5.4 Анализ условий безубыточности при изменениях цен

5.4

Анализ условий безубыточности при изменениях цен

Обращаясь к процедуре анализа приростной безубыточности, мы сосредоточиваем внимание лишь на изменении прибыльности в результате ценовых решений. Соответственно, точкой отсчета для менеджеров при проведении такого анализа становятся данные о текущих или проектируемых объемах продаж и уровнях прибыльности при ныне действующей (или ранее определенной) цене. И затем ставится вопрос: «Может ли изменение цены улучшить ситуацию?» Иначе этот вопрос можно сформулировать следующим образом: «Насколько объемы продаж должны возрасти, чтобы это компенсировало потерю выручки из-за снижения цен?» или «Насколько объемы продаж могут снизиться, чтобы не исчез прирост прибыли, обеспеченный повышением цены?»

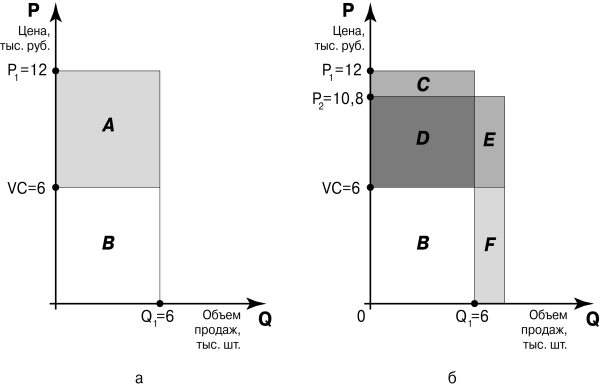
Рис. 5.2

Экономические последствия снижения цены

Пример

Ответы на такого рода вопросы зависят от величины относительного выигрыша, а процедуру поиска таких ответов мы рассмотрим на примере условной фирмы «Пластикон», выпускающей пластмассовые контейнеры для мусора.

Для фирмы «Пластикон» характерны следующие месячные показатели деятельности:

объем продаж, шт. 6000;

отпускная цена, тыс. руб. 12;

выручка от продаж, млн руб. 72;

переменные затраты, тыс. руб./шт. 6;

постоянные затраты, млн руб. 20.

Менеджеры фирмы недовольны объемом ее продаж и рассматривают целесообразность снижения цены на 10 % для его увеличения. Предполагается, что рост продаж (и соответственно выпуска) может быть обеспечен без увеличения постоянных затрат. Но насколько на самом деле должен возрасти объем продаж, чтобы компенсировать 10 %-ное снижение цены?

Для ответа на этот вопрос необходимо рассчитать безубыточное изменение продаж. При варианте снижения цен он будет представлять собой тот минимальный прирост продаж, который необходим, чтобы снижение цен привело к росту относительного выигрыша по сравнению с точкой отсчета.

Для наглядности рассмотрим рис. 5.2, на котором представлены экономические результаты фирмы «Пластикон» при различных уровнях цены.

A — суммарный выигрыш фирмы до изменения цены; B — переменные затраты фирмы на производство 6 тыс. ед. товара; C — потеря выигрыша в результате изменения цены; D — выигрыш, сохранившийся после изменения цены; E — прирост выигрыша в результате изменения цены; F — прирост переменных затрат в результате изменения цены; Q1 и Q2 — соответственно прежний и ожидаемый дополнительный объем продаж.

Как мы видим, при прежнем уровне цены (P1 = 12 тыс. руб.) «Пластикон» продавал 6 тыс. ед. товара в месяц. Это обеспечивало фирме объем реализации в сумме 72 млн руб. На графике 5.2а этой выручке соответствует сумма площадей прямоугольников A и B.

Из этой выручки «Пластикон» покрывал переменные затраты (variable cost, VC) в сумме 6 тыс. руб. на 1 ед. товара, или 36 млн руб. на весь месячный выпуск (площадь прямоугольника В). Следовательно, до изменения цены выигрыш «Пластикона» от продажи продукции составлял 36 млн руб. (72–36). Именно этой величине равна площадь прямоугольника А.

Отсюда мы можем сделать вывод: чтобы снижение цен оправдало себя, выигрыш после снижения цены должен быть в расчете на месяц больше 36 млн руб.

Чтобы понять, при каких условиях этот результат может быть достигнут, посмотрим на график 5.2б. Здесь изображена ситуация при снижении цены на 10 %, т. е. с 12 тыс. до 10,8 тыс. руб. (P2). Как мы видим, в расчете на прежний объем производства сокращение выигрыша «Пластикона» составит 7,2 млн руб. (1,2 тыс. руб./шт. ? 6 тыс. шт.).

Этой сумме соответствует площадь прямоугольника С. Тогда при прежнем объеме производства (продаж) выигрыш фирмы будет равен лишь 28,8 млн руб. (4,8 тыс. руб./шт. ? 6 тыс. шт.). Этой величине соответствует площадь прямоугольника D.

Изменения (в данном случае сокращения) выигрыша фирмы от продажи прежнего объема продукции при изменении цены называются эффектом цены.

Но поскольку мы имеем дело с нормальным товаром (величина спроса на который возрастает при снижении его цены], то справедливо ожидать, что удешевление товаров, продаваемых «Пластиконом», приведет к росту объемов их реализации. Однако величина выигрыша, который получит фирма в результате такого изменения ситуации (эффект объема], нам неизвестна.

Рассматривая рис. 5.2, пока можем сказать, что фирма выиграет от снижения цены, если выигрыш, полученный в результате проявления эффекта масштаба (его величина соответствует площади прямоугольника E], будет превышать потерю выигрыша в результате проявления эффекта цены (площадь прямоугольника С]. Иными словами, изменение цены оправдывает себя в том случае, если дополнительный выигрыш, полученный благодаря изменению объемов продаж, будет превышать сокращение выигрыша в расчете на прежний объем продаж из-за снижения цены. Соответственно, при повышении цены фирма достигнет лучших результатов в том случае, если дополнительный выигрыш от реализации продукции по более высокой цене превысит сокращение выигрыша из-за падения объемов продаж.

В этой ситуации задача анализа безубыточности состоит в определении того минимального прироста объемов продаж, который должен быть достигнут, чтобы влияние эффекта объема уравновесило влияние эффекта цены, т. е. чтобы площади прямоугольников С и Е оказались равны. Если же величина прироста выигрыша в результате проявления эффекта объема будет больше величины сокращения выигрыша в результате проявления эффекта цены, то снижение цены действительно приведет к росту прибыли фирмы.

Как же определить безубыточный прирост продаж?

Мы установили, что сокращение выигрыша «Пластикона» в результате снижения цены составит 7,2 млн руб. (именно этой величине равна площадь прямоугольника С]. Соответственно, и величина выигрыша в результате проявления эффекта объема должна составить ту же сумму (прямоугольник Е].

Нетрудно рассчитать, что после снижения цены выигрыш «Пластикона» с каждого проданного контейнера составит 4,8 тыс. руб. (10,8–6,0]. Значит, чтобы суммарный выигрыш от увеличения объема продаж уравнялся с потерей выигрыша в результате снижения цены, «Пластикон» должен продавать дополнительно 1,5 тыс. контейнеров (7,2 млн руб.: 4,8 тыс. руб./шт.].

Величина минимального прироста продаж, необходимого для сохранения прежней общей суммы выигрыша после изменения цены, может быть рассчитана с помощью следующей формулы:

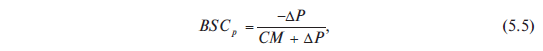
где BSCp — безубыточный прирост продаж в результате изменения цены,

% [break-even sales change];

Р — изменение цены (указывается с учетом знака, а именно:

«+» при повышении цены и «?» при снижении цены];

CM — удельный выигрыш.

В этом уравнении величины изменений цен и выигрыша могут быть выражены любым, но одинаковым образом (в абсолютных величинах, в процентах или десятичных дробях]. В итоге мы все равно получим процентный показатель того, на сколько должно измениться число продаваемых изделий, чтобы и после изменения цены общая сумма выигрыша фирмы осталась неизменной.

Минус в числителе этого уравнения напоминает нам об альтернативе, с которой связано изменение цены: ее увеличение ведет к сокращению не только числа продаваемых изделий, но и числа изделий, которые надо продать, чтобы достичь нужной массы прибыли. Напротив, снижение цены ведет не только к росту числа продаваемых изделий, но и к увеличению числа изделий, которые надо суметь продать, чтобы достичь нужного уровня прибыльности.

Чем больше масштаб снижения цены, тем более существенно надо прирастить число продаваемых изделий, чтобы сохранить хотя бы прежнюю общую величину выигрыша фирмы от продажи такого товара.

Вернемся для пояснения этой мысли к рассмотренной ситуации и предположим, что намечаемое фирмой «Пластикон» снижение цены на 10 % не повлечет для нее прироста переменных и постоянных издержек. Тогда, используя формулу (5.3) для расчета удельного выигрыша и ведя расчет в абсолютных величинах, мы получим следующую величину удельного выигрыша CMa этой фирмы до снижения цены:

CMa = 12 тыс. руб. — 6 тыс. руб. = 6 тыс. руб.

На этой основе мы можем теперь без труда рассчитать тот прирост числа контейнеров, которого надо добиться «Пластикону», чтобы оправдать снижение цены на 10 %:

BSCp = [— (—1,2 тыс. руб.)]: [6 тыс. руб. + (—1,2 тыс. руб.)] х 100 = 25 %

или в относительном выражении:

BSCp = [— (—10 %)]: [50 % + (—10 %)] х 100 = 25 %.

Таким образом, 10 %-ное снижение цены окупится для «Пластикона» лишь в том случае, если число продаваемых контейнеров возрастет на 25 % (что соответствует уже полученному нами выше результату — прирост в 1,5 тыс. шт. составляет как раз 25 % прежнего объема продаж в 6000 шт.).

Таким образом, безубыточный прирост продаж (в абсолютном выражении) может быть найден с помощью формулы:

BSCa = (BSCp х S0): 100, (5.6)

где BSCa, BSCp — безубыточный прирост продаж при изменении цен, соответственно в абсолютном и процентном выражении;

S0 — объем продаж до изменения цен, нат. ед. (в нашем примере он составит 0,25 х 6 тыс.= 1,5 тыс. шт.).

Соответственно, если реальный прирост объема продаж превышает величину безубыточного прироста, то фирма не только ничего не теряет в результате изменения цены, но даже получает дополнительную прибыль. И эта логика существенно может влиять на формирование коммерческой политики фирмы.

Скажем, если руководство фирмы «Пластикон» на данном этапе заинтересовано преимущественно в захвате большей доли рынка, а не в увеличении массы прибыли, то оно может пойти на снижение цены даже в том случае, если прирост числа продаваемых контейнеров не превысит безубыточного количества (в нашем случае 1,5 тыс. шт.). Напротив, если основной задачей фирмы в данном периоде является максимизация прибыли, то она может идти на снижение цен лишь в том случае, если имеются веские основания ожидать роста числа продаваемых контейнеров более чем на 25 %.

Оценку влияния изменения объемов продаж на величину выигрыша фирмы можно сделать очень просто. Для этого надо лишь умножить разницу между реально достижимым после изменения цены объемом продаж и безубыточным объемом продаж на новую величину удельного выигрыша (т. е. ту величину, которая сложится после изменения цен].

Теперь предположим, что после изменения цены объем продажу «Пластикона» возрастет на 1,7 тыс. шт. Что касается новой величины удельного выигрыша, то она в соответствии с формулой (5.3] будет равна 4,8 тыс. руб. (10,8 тыс. руб. — 6 тыс. руб.].

Тогда прирост прибыли этой фирмы составит:

(1,7 тыс. шт. — 1,5 тыс. шт.) х (10,8 тыс. руб. — 6 тыс. руб.) = 960,0 тыс. руб.

Точно такая же логика используется и при анализе изменений цен, связанных с их повышением.

Данный текст является ознакомительным фрагментом.