4.2. Как определять размер скидки и прогнозировать объем продаж при ценовом стимулировании

4.2. Как определять размер скидки и прогнозировать объем продаж при ценовом стимулировании

Скидки могут предоставляться исходя из различных целей стимулирования, некоторые из них не связаны с увеличением прибыли от продаж того товара, на который они назначены. На рисунке 4.7 показаны типы скидок в зависимости от целей стимулирования.

Скидки на товары при распродажах и скидки «убыточный лидер» являются экономией лишь для покупателей, для предприятия это – затраты на стимулирование других товаров. Размеры убытков, связанные с продажей товаров по ценам, которые почти всегда ниже себестоимости, включаются в бюджет на стимулирование других товаров, приносящих предприятию дополнительную прибыль.

Рассмотрим вопрос о стимулирующих скидках. Размер скидки, который приведет к увеличению объемов продаж и к увеличению прибыли, зависит от многих параметров:

• эластичность спроса по цене и оптимальная цена на товар;

• цены конкурентов и доступность их товаров для потребителей;

• неценовые факторы увеличения/снижения спроса;

• потенциал спроса (емкость рынка);

• наличие необходимого объема товара для его удовлетворения.

Кратко рассмотрим теорию цены. Вопрос эластичности спроса и оптимальной цены исследован достаточно подробно. Эластичность спроса по цене между двумя точками кривой спроса от точки 2 (большя цена без стимулирования) до точки 1 (меньшая цена при стимулировании), как показано на рис. 4.8, определяется следующим образом:

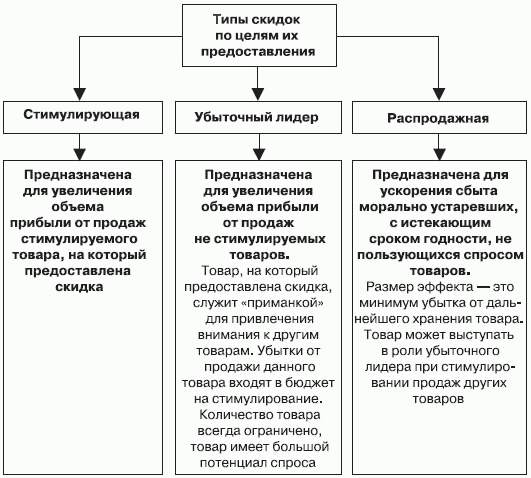
Рис. 4.7. Типы скидок в зависимости от целей стимулирования

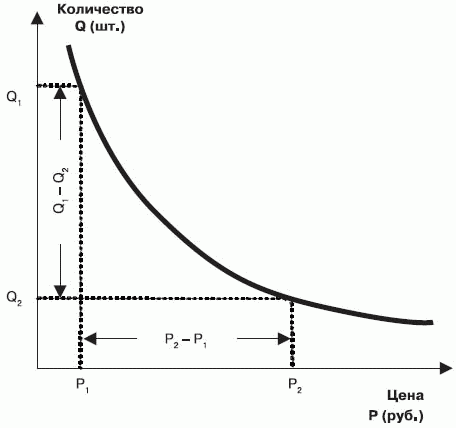
Рис. 4.8. Определение эластичности спроса по цене

Эластичность показывает темп прироста объема продаж в натуральном выражении при снижении цены. Величина е показывает, на сколько процентов увеличивается спрос при снижении цены на один процент на участке кривой спроса от точки 2 до точки 1 или в предельном случае – в любой точке непрерывной гладкой кривой спроса. Можно сформулировать иначе: на сколько процентов уменьшается спрос при увеличении цены на один процент. Здесь интересна не сама формула, а следствие из нее, касающееся изменения объемов выручки при изменении цены.

Различают три вида спроса: эластичный, нейтральный и неэластичный. При неэластичном спросе, когда эластичность по модулю меньше единицы ( – 1 <e < 0), так же, как и при нейтральном спросе, когда она равна по модулю единице, при снижении цен будет наблюдаться снижение выручки (P₁Q₁?P₂Q₂), а при увеличении цены – увеличение выручки. Такая ситуация рассматривалась в примере 3.4 (раздел 3.3): цена растет, количество проданных холодильников в штуках падает (закон спроса), но выручка увеличивается (неэластичный спрос).

С точки зрения стимулирования более всего интересна ситуация эластичного спроса, когда показатель эластичности больше единицы по модулю или меньше минус единицы по значению (e< —1). В этом случае снижение цен приводит к увеличению выручки (P₁Q₁>P₂Q₂), но еще не к увеличению прибыли. Для того чтобы искать оптимальную цену, дающую максимум прибыли при эластичном спросе, необходима функция затрат, о чем мы поговорим ниже.

На рисунке 4.9 графически показаны ситуации эластичного, нейтрального и неэластичного спроса.

Рис. 4.9. Неэластичный, нейтральный и эластичный спрос

Площадь прямоугольника, ограниченного ценой и объемом продаж, в натуральном выражении показывает объем выручки; очевидно, когда выручка растет, а когда уменьшается. В таблице 4 Л и примере 4.5 представлены ситуации различного по эластичности спроса.

Пример 4.5

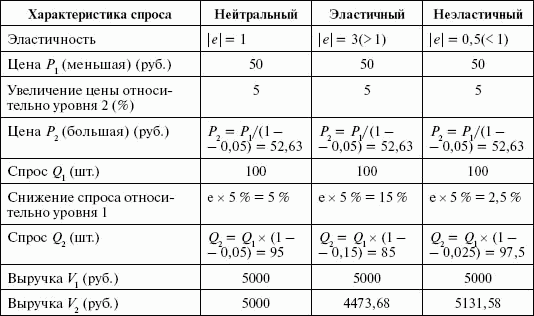
Комментируем табл. 4.1. Допустим, вы продаете персики по цене 50 руб. за килограмм в количестве 100 кг в неделю. Каков будет спрос в натуральном выражении и выручка в деньгах, если цена – 52,63 руб. (на 5 % больше) при различных видах спроса по эластичности? Вопрос можно сформулировать иначе: каков спрос по эластичности, если при цене на 5 % выше мы будем продавать 95, 85 и 98 кг в неделю (см. табл. 4.1).

Ситуация первая. Спрос нейтральный – выручка не меняется. При увеличении цены на 5 %, спрос в точке 2 меньше спроса в точке 1 на те же 5 % и составляет 95 кг. Выручка в обеих точках равна 5 тыс. руб. Сразу отметим одну тонкость в формуле эластичности. За базу цены, относительно которой считается скидка или надбавка, принимается цена в точке 2 (большая), а за базу количества продаваемого товара – точка 1, также с большим объемом. Ситуация вторая. При эластичном спросе на каждый процент снижения цены спрос увеличивается на 3 %, т. е. при цене на 5 % меньше спрос будет на 15 % больше. При цене 52,63 руб. за килограмм мы будем продавать 85 кг, при цене 50 руб. за кг – на 15 % больше (на каждый из 5 % цены получаем увеличение спроса на 3 %, итого 15 %), т. е. 100 кг (100 кг минус 15 % – 85 кг). Выручка при меньшей цене составит 5 тыс. руб., при большей цене – 4473,68 руб. Ситуация третья. Спрос неэластичный. На каждый процент увеличения цены получаем всего 0,5 % снижения спроса. При цене 50 руб. продаем 100 кг, выручка 5 тыс. руб. При цене 52,63 руб. продаем 97,5 кг, выручка – 5131,58 руб.

Таблица 4.1

Различные виды спроса по эластичности

Если обозначить через k величину темпа прироста (снижения) цены в точке 2 относительно этой же точки в виде десятичной дроби, то величину темпа прироста выручки d в натуральном выражении при известной эластичности е можно рассчитать по приведенной ниже формуле. Также можно перевести величину темпа прироста k в величину темпа прироста n цены в точке 2 относительно цены в точке 1:

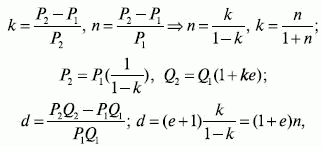
где k – темп прироста цены P₂ относительно цены P₂ (скидка), ед.; п – темп прироста цены P₂ относительно цены Р_1, ед.; d– темп прироста объема продаж в точке 2 относительно точки 1, ед.

Можно вычислить и точку оптимальной цены при максимизации прибыли при эластичном спросе без ограничений на объем продаж в натуральном выражении и найти оптимальные объем продаж и размер прибыли при фиксированной эластичности на всем участке кривой спроса. Для этого необходима функция затрат или себестоимости. Далее, согласно правилам нахождения экстремума функции одной переменной без ограничений с помощью дифференцирования и приравнивания первой производной к нулю, находим точку оптимальной цены, дающей максимальную прибыль:

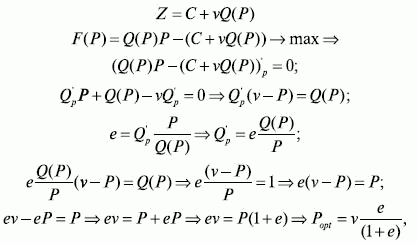
где Z– затраты (себестоимость) на производство и реализацию продукции, руб.; C – постоянные затраты, не зависящие от объема производства и реализации, руб.; v – переменные затраты на единицу продукции, руб.; Q(P) – объем продаж в штуках, зависит от цены; P – цена, руб.; F(P) – прибыль, руб., зависит от цены; е – эластичность спроса по цене, меньше – 1; P_opt – оптимальная цена, максимизирующая прибыль, руб.

Экстремум будет точкой максимума, так как при эластичном спросе прибыль является выпуклой функцией (выпуклостью вверх) как сумма двух выпуклых функций – выручки и затрат. Формула оптимальной цены справедлива, если в процессе снижения цены не изменяются ни переменные, ни постоянные затраты, и эластичность – постоянная величина в любой точке, не зависящая ни от каких переменных. В реальной ситуации это практически невозможно.

По данным Ж. Ж. Ламбена [53], общий обзор исследований для западных стран дает оценку для е от – 1,6 до – 2,5, если говорить об эластичном спросе.

Наибольшее применение в практике среди явных функций спроса получила степенная функция зависимости объема продаж от цены, имеющая постоянную эластичность спроса на всем участке кривой:

Q = A x Р^Е.

Эластичность в данном случае – это показатель степени E:

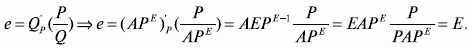
Между двумя точками (Q₁P₁) и (Q₂P₂) эластичность e постоянна и определяется по следующей формуле:

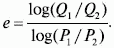
Эластичность спроса по цене определяется в ходе экспериментов или опросов покупателей. При проведении экспериментов необходимо учесть:

• цены конкурентов;

• размеры скидок, обычно применяемые в отрасли при проведении мероприятий по стимулированию;

• наличие рекламы на месте продажи;

• другие посторонние факторы.

Функция спроса не является гладкой на всем исследуемом промежутке цены. Спрос может быть неэластичным, если мы двигаемся в интервале цены, не превышающей цену конкурента, и стать резко эластичным при пересечении границы конкурентной цены (рис 4.10). Поэтому необходимо проводить хотя бы один эксперимент при цене ниже, чем у конкурентов, если они существуют.

Пример 4.6

Вы продаете телевизоры определенной марки с определенными техническими характеристиками по цене 10 тыс. руб. Конкурент, который находится напротив вас, продает те же телевизоры по цене 8 тыс. руб. Вы снижаете цену до 9,5 тыс., 9 тыс., 8,5 тыс., 8 тыс. руб. за шт., но количество покупателей не становится существенно больше, и выручка не растет (неэластичный спрос). Однако, как только вы устанавливаете цену 7,9 тыс. руб., в кассу образуется очередь, и выручка резко вырастает.

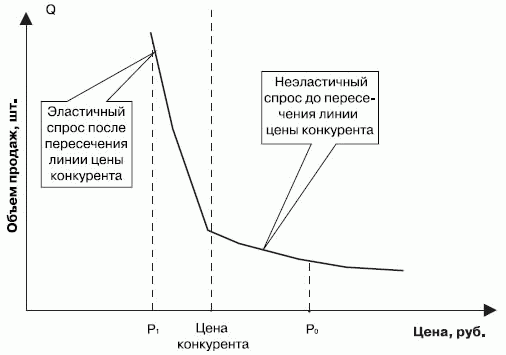
Рис. 4.10. Эластичность спроса в зависимости от цены конкурента

Цена ниже, чем у конкурентов, может и не быть оптимальной, т. е. не давать максимума прибыли. Принятая цена может быть как выше, так и ниже оптимальной. Если она ниже оптимальной, то следует не предоставлять скидки, а увеличивать цену. Более того, если мы боремся с конкурентами с помощью цен, она может стать ниже наших переменных затрат, т. е. ниже закупочной цены, как говорят в торговле.

Если мы уверены в объеме реализации любого объема товара при конкурентоспособной цене, можно определить безубыточный минимальный объем реализации, позволяющий окупить постоянные и переменные затраты:

где Z – затраты (себестоимость) на производство и реализацию продукции, руб.; C – постоянные затраты, не зависящие от объема производства и реализации, руб.; v – переменные затраты на единицу продукции, руб.; Q – объем продаж в штуках, может быть сколь угодно большой; Q^* – безубыточный объем производства, в штуках; P – цена, руб.; F – прибыль, руб., равно нулю в точке безубыточности.

На рисунке 4.11 показана точка безубыточности (безубыточный объем производства и реализации при заданной цене).

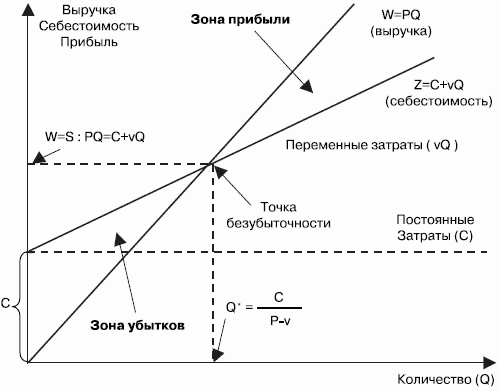
Рис. 4.11. Безубыточный объем производства и реализации

Разность между ценой и переменными издержками, которая стоит в знаменателе формулы, определяющей безубыточный объем производств и реализации, называется маржинальным доходом, маржинальной прибылью или просто маржой. В торговле, где основной объем переменных затрат приходится на закупочную цену, маржа – это торговая наценка, разность между ценой реализации и закупочной ценой, возможно, включающей транспортные расходы.

Исходя из формулы нулевой прибыли и точки безубыточности, можно определить минимальную затратную цену при реализации определенного, фиксированного объема товара при нулевой прибыли. Для того чтобы цена была минимальной, объем реализации должен быть максимально возможным:

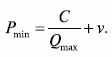
Если мы установили для себя норматив маржинальной прибыли в процентах к закупочной цене, то можем определить затратную цену при фиксированном целевом объеме производства и реализации:

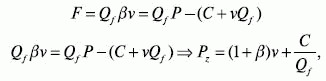
где ? – норматив маржинального дохода в долях от 0 до 1; Q_f – целевой, фиксированный объем производства и реализации, шт.

Кроме переменных затрат, которые согласно теории затратного ценообразования должны приносить прибыль, у нас еще есть постоянные затраты, которые тоже должны приносить прибыль. Большинство статей постоянных затрат (амортизация, аренда, проценты за кредит и т. п.) относятся к категориям инвестиционных затрат, и в качестве норматива эффективности издержек к ним применяется ставка процента по инвестициям в год. Исходя из нее можно получить дополнительный прирост прибыли за счет использования постоянных затрат. С учетом ставки по инвестициям, пересчитанной на соответствующий период производства и реализации, затратная цена будет выглядеть следующим образом:

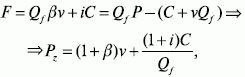
где i – норматив эффективности инвестиций в долях от 0 до 1.

Если прибыль является просто фиксированной величиной, не зависящей от объема переменных и постоянных затрат, формула затратной цены будет выглядеть следующим образом:

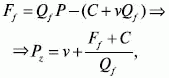
где F – фиксированный (целевой) размер прибыли (руб.).

На рисунке 4.12 показан график зависимости прибыли от цены при эластичном спросе.

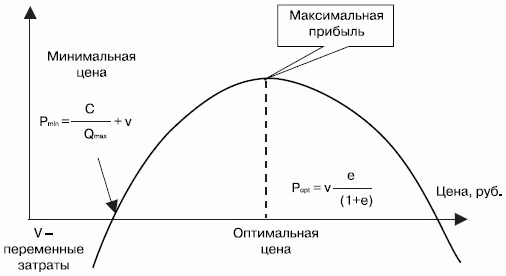
Рис. 4.12. Зависимость прибыли от цены при эластичном спросе

Рассмотрим пример стимулирования продаж остатка товара, который нам придется утилизировать в связи с истечением срока годности, с применением теории затратной цены.

Пример 4.7

Гипермаркеты «О`КЕЙ» в Санкт-Петербурге предлагают своим покупателям широкий выбор салатов. Все салаты готовятся утром и в течение дня и должны быть проданы до 23.00 (время закрытия магазина), в противном случае их утилизируют. Часто, но не всегда, покупатели, пришедшие в магазин вечером около 20.00 – 21.00, могут услышать объявление по радио, что с 22.00 до 23.00 все салаты будут продаваться со скидкой 50 %.

Для простоты мы рассмотрим ситуацию с одним условным салатом, который назовем «Оливье». Для его производства требуется колбаса, картофель, огурцы, лук, зеленый горошек, майонез и соль. По опыту, в течение дня при различных ценах за килограмм мы можем продать максимально 100 кг салата, минимально – 10 кг. В среднем по всем дням продаж в течение месяца с учетом сезонности – 50 кг. Для производства салата на один килограмм нам необходимо определенное количество продуктов, и затраты на их приобретение показаны в табл. 4.2. Это будут наши переменные затраты на единицу продукции (1 кг салата).

Таблица 4.2

Переменные затраты на производство 1 кг салата с учетом отходов

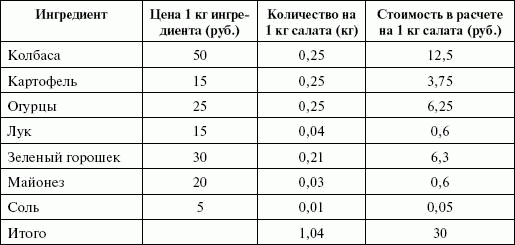
Кроме переменных еще есть постоянные затраты в расчете на день, не зависящие от объема продаж, которые приведены в табл. 4.3

Таблица 4.3

Постоянные затраты на производство и реализацию салата в течение дня

Мы планируем средний объем производства в количестве 50 кг плюс 25 кг – среднее отклонение вверх от среднего значения в день, итого 75 кг. Прибыль планируется исходя из наценки (маржи) 25 % на сумму переменных затрат при реализации среднего объема – 50 кг. Таким образом, сумма прибыли, которая в принципе рассчитана на 50 кг, должна составить в день 375 руб., объем затрат (себестоимость) на 75 кг – 3250 руб., а затратная цена за килограмм салата в расчете на 50 кг составит 73 руб. за кг (табл. 4.4).

Таблица 4.4

Целевая прибыль и затратная цена

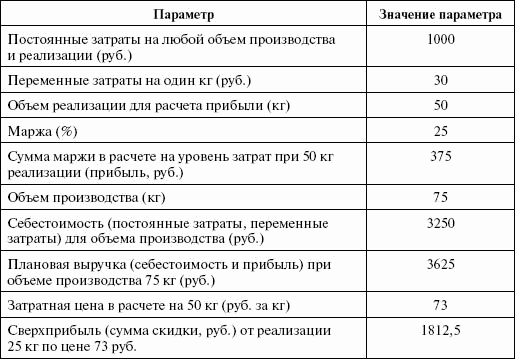
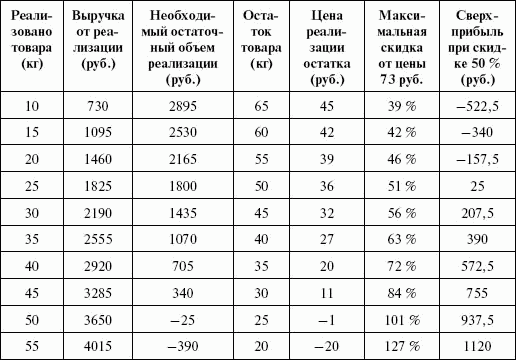
Если в какой-то момент времени продано 50 кг, то весь оставшийся объем можно отдать даром: мы компенсировали затраты на производство 75 кг салата и получили целевую прибыль. Когда же нам выгодно предоставить 50 % скидки? В таблице 4.5 показаны расчеты максимальных скидок на различный объем остатка товара и дополнительная прибыль при скидке в 50 % при плановой выручке 3625 руб.

Таблица 4.5

Размеры скидок и дополнительная прибыль

На разных рынках существуют различные стандарты на предоставление скидок в мероприятиях по стимулированию. В таблице 4.6 приведены данные, собранные автором по размерам скидок, предоставляемых при проведении мероприятий по стимулированию на разные группы товаров в Санкт-Петербурге в 2005 г.

Таблица 4.6

Размеры скидок при проведении мероприятий по стимулированию на разные группы товаров в Санкт-Петербурге в 2005 г.

Верхняя граница скидок определяется средней величиной доли переменных затрат в отрасли, а эффект воздействия цены – эластичностью, известной после проведения эксперимента. Для подготовки мероприятия по стимулированию эксперимент следует проводить при наличии рекламы на месте продажи, чтобы не учитывать этот фактор при определении влияния массовой коммуникации.

Объем продаж зависит не только от величины скидки (ценовой фактор, определяемый эластичностью), но и от масштаба массовой коммуникации, который является неценовым фактором. На рисунке 4.13 показан вид функции зависимости объемов продаж при ценовом стимулировании с учетом неценового сдвига под влиянием коммуникации. При одной и той же цене можно получить разный дополнительный объем продаж, который обеспечивается различными уровнями коммуникации.

В общем случае эффект воздействия массовой коммуникации определяется охватом целевого рынка при эффективной частоте, которая определяет отклик покупателей на воздействие конкретных средств коммуникации [72, 75]. С учетом того, что мероприятия по стимулированию имеют самый высокий рейтинг среди предметов коммуникации по краткосрочному эффекту воздействия на объемы продаж, эффективная частота будет минимальной. Для печатных СМИ, как мы предполагаем, она составит 1+ (минимум один контакт с рекламным объявлением), для вещательных (телевидение и радио) – 3+ (минимум три контакта) [75]. При проведении стимулирования эластичность выступает как усилитель эффекта охвата.

Эффект различных средств рекламы по привлечению в магазины розничной торговли может быть изучен с помощью опросов.

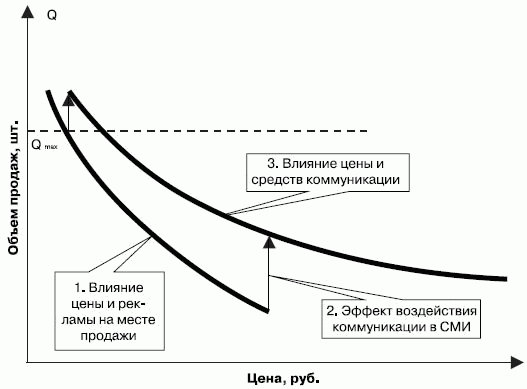
Рис. 4.13. Функция зависимости объемов продаж при ценовом стимулировании

Пример 4.8

В ходе исследования [32], проведенного фирмой «ГОРТИС» для супермаркетов электроники «ТЕЛЕМАКС» в 2004 г., получены следующие данные: «Результаты опроса посетителей и покупателей магазинов „ТЕЛЕМАКС“, так же как и результаты опроса жителей Санкт-Петербурга, подтверждают наибольший коммуникативный эффект (в период, предшествующий исследованию) от рекламы и распространения фирменной газеты и рекламы на щитах. Газета – эффективное средство информирования, так как получение газеты подтверждают почти 30% жителей Санкт-Петербурга. Газета – эффективное средство формирования спроса: почти 30% посетителей магазинов „ТЕЛЕМАКС“ утверждают, что она повлияла на выбор магазина для посещения, т. е. „привела“ их в магазин».

Эффект воздействия коммуникации в СМИ и рекламы на месте продажи при стимулировании продаж аптечных товаров описан в [37] (пример 4.9).

Пример 4.9

Эффективность стимулирования сбыта в аптечном бизнесе повышается при координации его мероприятий с рекламной кампанией. Как показывают исследования, ценовое стимулирование, проведенное одной из аптек, увеличило объем продаж лишь на 15 %. В сочетании с рекламой показатель вырос на 19 %, а в комплексе с рекламой и демонстрацией товара на месте продажи – на 24 %.

Конкретный вид функции отклика на бонус (скидку) и коммуникацию различен в зависимости от анализируемой ситуации. Для рассмотренных выше ситуаций, связанных с магазинами бытовой техники и аптекой, автор предлагает следующий вид несложной функции отклика покупателей для прогнозирования объемов продаж при стимулировании:

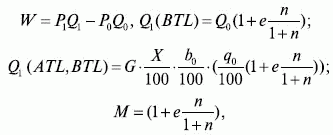
где Q₁ – объем продаж товара при проведении мероприятия по стимулированию, шт.; Q₁(BTL) – объем продаж при стимулировании и рекламе на месте продажи, шт.; Q₁(ATL, BTL) – объем продаж при стимулировании, массовой рекламе и рекламе на месте продажи, шт.; G – количество семей, планирующих покупку товара, шт.; X– охват целевого рынка, проценты; b₀ – доля продаж рассматриваемого товара во всем ассортименте товарной категории при постановке эксперимента, проценты; q₀ – доля покупателей среди посетителей, проценты; M – коэффициент роста, зависящий от эластичности спроса e, ед.

В данной модели коэффициент используется один раз для мультипликации (усиления) влияния доли покупателей среди всех посетителей. Он может использоваться и дважды – дополнительно для усиления эффекта доли охвата, если эффективный охват был ранее измерен без условий стимулирования. Тогда итоговая формула оптимистического прогноза будет выглядеть следующим образом:

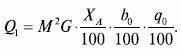
Рассмотрим приведенные выше формулы на примере стимулирования продаж стиральных машин ARISTON (название марки взято исключительно для примера) в условной сети магазинов бытовой электроники с использованием реальных данных опросов.

Пример 4.10

Рассмотрим результаты опроса жителей Санкт-Петербурга в возрасте от 16 до 60 лет по планированию покупок бытовой техник (табл. 4.7 [32]).

Таблица 4.7

Планирование покупок бытовой электроники. «Какой товар Вы планируете приобрести в ближайшие полгода?»

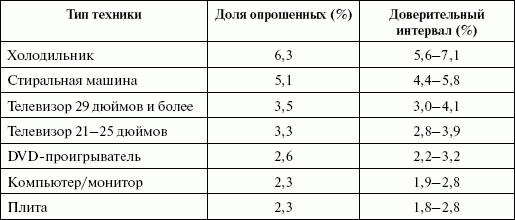
Для крупных покупок, осуществление которых часто планируется заранее, можно говорить, что холодильники приобретет не менее 70 тыс. семей, стиральную машину – не менее 60 тыс. семей, плиту – не менее 25 тыс. семей, телевизор 29` и более – не менее 40 тыс. семей, телевизор 21 – 25` – также не менее 40 тыс. семей. Руководство магазина приняло решение провести акцию по ценовому стимулированию стиральных машин ARISTON. Сначала поставили эксперимент со снижением цены и рекламой на месте продаж в течение месяца на эти стиральные машины. При цене 15 тыс. руб. за месяц продавалось 49 машин, при цене 14 тыс. руб. была продана 61 машина. Эластичность составила – 3,4. В таблице 4.8 приведено распределение продаж стиральных машин в сети магазинов бытовой техники до и после проведения эксперимента по снижению цен (цифры условные).

Затем было решено задействовать для рекламы снижения цен фирменную газету-каталог, распространяемую бесплатно по почтовым ящикам. Для прогнозирования объема продаж использовалась вышеприведенная модель, данные опроса потенциальных покупателей, данные эксперимента со снижением цены и информация об охвате целевого рынка рекламного воздействия фирменной газетой-каталогом, которая обеспечивает охват 30 % петербуржцев (см. пример 4.8). В таблице 4.9 приведен расчет прогноза объема продаж.

Таблица 4.8

Распределение долей по продажам стиральных машин

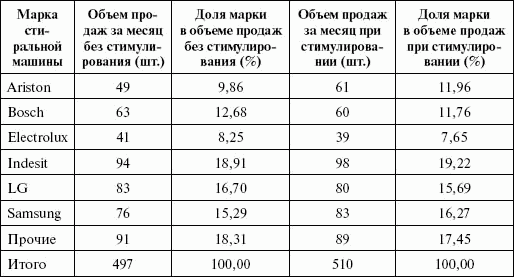
Таблица 4.9

Расчет прогнозов продаж при ценовом стимулировании

Предложенная модель, безусловно, не может применяться для прогнозирования объема продаж чего угодно в любых условиях. В каждом конкретном случае модель прогнозирования строится исходя из специфических характеристик рынка и факторов, определяющих решение о покупке и характер рекламного воздействия.

Отметим, что на наш взгляд при проведении мероприятий как ценового, так и неценового стимулирования больший вклад в прирост продаж дает не скидка (бонус), а коммуникация, обеспечивающая привлечение покупателей на место продажи.

На практике скидки, как правило, не являются проверенными в экспериментах стимулами к увеличению объема продаж. Заявляя, например, в телевизионной рекламе «Скидка на ВСЕ 50 %!» в углу экрана мелким шрифтом помещают уточнение: «На все модели с красными ценниками». Понятно, что скидка дается лишь на две модели, а на все остальные скидок нет. Так как эта информация, хотя и мелким шрифтом, содержится в рекламе, то закон «О рекламе» вроде бы и не нарушается, а размер шрифта закон не оговаривает. Как вы понимаете, мелкий шрифт не особенно актуален в телевизионной рекламе. Количество рекламного товара ограничено, никто не ожидает прибыли от продажи этих моделей. Назовем такой товар и систему привлечения «бесплатный сыр». Этот механизм привлечения людей в магазин – опасен, но в нашей стране он пока работает.

Из перечисленных в начале этого раздела факторов, которые влияют на увеличение объемов продаж и прибыли при стимулирующих скидках, остались два: потенциал спроса и наличие товара для его удовлетворения. Достичь максимальной прибыли можно только при наличии определенной величины спроса в натуральном выражении с одной стороны, и наличии товара, способного удовлетворить это спрос, с другой стороны. Многие мероприятия по стимулированию убыточны именно по этим причинам. Предприниматели планируют продать много товара, но он не нужен ни в таком количестве, ни по такой цене. Обидно также бывает, когда в магазин стоит очередь, а товара уже нет и не будет: не запланировали, не выпустили, вовремя не заказали, не подвезли... При стимулировании вопросы логистики не менее важны, чем вопросы коммуникации.

Данный текст является ознакомительным фрагментом.