5.3.1. Модели
Модель лексикографического упорядочения
Пусть критерии K1…, Ks, по которым оцениваются объекты принятия управленческих решений, таковы, что K1 существенно важнее всех остальных частных критериев, K2 важнее всех остальных частных критериев, за исключением K1, и т. д. В этом случае если альтернативный вариант ai предпочтительнее альтернативного варианта aj по частному критерию K1, то независимо от их оценок по остальным критериям альтернативный вариант ai более предпочтителен, чем вариант aj. Если же оценки альтернативных вариантов совпадают по первым r критериям и различаются по критерию (r + 1), то более предпочтительным в этом случае является альтернативный вариант, который более предпочтителен по критерию (r + 1).
Такая модель сравнительной оценки альтернативных вариантов управленческих решений по предпочтительности называется лексикографической.
Легко заметить, что при использовании модели лексикографического упорядочения все альтернативные варианты оказываются строго проранжированными, если не считать альтернативные варианты с полностью совпадающими оценками по всем критериям.
При использовании данной модели задача выбора наиболее предпочтительного альтернативного варианта или даже нескольких из них для управленца или эксперта не составляет труда. Для этого достаточно выбрать нужное число первых альтернативных вариантов в их лексикографическом упорядочении.
Модель обобщенного критерия
Однако далеко не всегда частные критерии оценки альтернатив K1…, Ks, настолько неравноценны по важности, чтобы можно было использовать модель лексикографического упорядочения. Более типична ситуация, когда относительная важность критериев, по которым осуществляется сравнительная оценка альтернативных вариантов управленческого решения, является сопоставимой.
В этом случае могут использоваться различные методы «свертки», позволяющие производить сравнительную оценку при использовании моделей обобщенного критерия и дать единую численную оценку каждому из сравниваемых альтернативных вариантов.
Одним из наиболее важных предположений при установлении факта сопоставимости критериев является предположение об их независимости.
Для случая s= 2 (двух критериев) свойство независимости критериев может быть сформулировано следующим образом:
(xi1, xi2) p (xi1, xj2) ? (xi1, xj2) p (xj1, xj2), (5.1)
(xi1, xi2) p (xi1, xj2) ? (xj1, xi2) p (xj1, xj2), (5.2)
где xi1 и xj1 – значения оценок альтернативных вариантов ai и aj по критерию K1;
xi2 и xj2 – значения оценок альтернативных вариантов ai и aj по критерию K2.
Соотношение (5.1) показывает, что предпочтения альтернатив сохраняются при любых одинаковых значениях оценок по критерию K2 и определяются оценками по K1, а соотношение (5.2) показывает, что предпочтения альтернативных вариантов сохраняются при любых одинаковых значениях по критерию K1 и определяются оценками по K2.
Однако сформулированные условия независимости критериев оказываются необходимыми, но не достаточными для существования обобщенных критериев.
Необходимые и достаточные условия существования функций полезности u1(x)…, us(x) таковы, что альтернативный вариант ai предпочтительнее варианта aj, когда
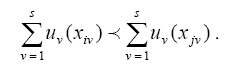
Исследованию функций ценности (полезности) 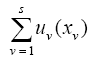 посвящена обширная литература (см., напр., [7, 12]).
посвящена обширная литература (см., напр., [7, 12]).
Нас прежде всего интересуют методы формирования обобщенных критериев, используемые при анализе и обработке экспертной информации, к которой относятся и оценки управленца, и оценки экспертов.
Модель линейного обобщенного критерия предполагает использование критериев, обладающих свойством аддитивности и сопоставимости их по относительной важности. Случай, когда одни из критериев существенно важнее остальных, приводит к лексикографическому упорядочению критериев, рассмотренному выше. Заметим, что сравнивать по предпочтительности имеет смысл лишь однородные критерии, характеризующие критерии одной природы. В случае когда критерии таковыми не являются, необходимо их преобразовать в однородные.
Если измерения по критериям произведены в шкалах отношений, оценки по ним преобразовываются по формуле

где 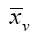 – максимально возможная оценка по v-му критерию.
– максимально возможная оценка по v-му критерию.
Если измерения по критериям произведены в шкалах интервалов, оценки преобразовываются по формуле
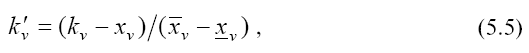
где 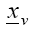 – минимальная оценка по v-му критерию [9].
– минимальная оценка по v-му критерию [9].
Непротиворечивость критериев позволяет получать непротиворечивую информацию о сравнительной предпочтительности альтернативных вариантов при экспертном оценивании. Измерение критериев в шкале порядка не позволяет корректно вводить операции сложения оценок по различным критериям.
Модель обобщенных линейных критериев широко применяется в практике управления при многокритериальной оценке альтернативных вариантов управленческого решения. При ее использовании предполагается определение весовых коэффициентов c1…, cs , критериев K1…, Ks, содержащих информацию о сравнительной важности критериев.
При применении модели обобщенных линейных критериев сравнительная оценка оцениваемых по нескольким критериям альтернативных вариантов может быть определена с помощью обобщенного линейного критерия

Наиболее предпочтительным признается альтернативный вариант ai0, для которого справедливо следующее соотношение:
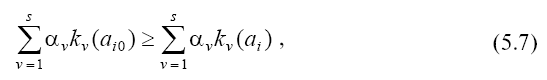
где i ? {1…, n}.
Если необходимо выбрать к наиболее предпочтительных альтернативных вариантов, то ими будут к альтернативных вариантов, получивших наибольшие оценки по критерию (5.5).
Обобщенный линейный критерий (5.5) существует, когда значения критериев максимального уровня измеримы по шкале отношений (т. е. по шкале, аналогичной той, в которой измеряются вес, длина и т. д.).
Если обобщенный критерий построить не удается, следует пользоваться другими моделями сравнительной оценки многомерных альтернативных вариантов.
Нередко при оценивании проектов возникает необходимость в использовании критериев, оценки по которым могут быть получены лишь с помощью специально разрабатываемых вербально-числовых шкал. В этом случае полезными оказываются модели сравнительной оценки альтернативных вариантов управленческого решения, в которых используются вербально-числовые шкалы. В состав вербально-числовых шкал входят, как правило, содержательное описание градаций шкалы и числовые значения, соответствующие каждой из ее градаций.
В качестве примера вербально-числовой шкалы, имеющей достаточно широкое применение, приведем имеющую универсальный характер шкалу Харрингтона (табл. 5.11).
Численные значения градаций шкалы Харингтона получены на основе анализа и обработки большого массива статистических данных. Она может использоваться при оценке альтернативных вариантов управленческого решения по критериям, допускающим лишь субъективную оценку управленца или эксперта.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКДанный текст является ознакомительным фрагментом.