6.5.2. Коэффициентирование категории «качество»
6.5.2. Коэффициентирование категории «качество»
Самый распространённый пример перевода количественных характеристик в качественные – это запись чисел в разрядной сетке позиционных систем счисления. До определённого момента, зависящего от используемого основания системы счисления, позиция записи цифр не меняется. В десятичной системе цифры от 0 до 9 пишутся в одной и той же позиции. Но число 10 в десятичной системе уже нельзя записать в той же позиции. Для его записи требуется создание новой ячейки разрядной сетки, в которую теперь будут записываться не числовые «единицы», а качественно новые «десятки». Набор цифр будет тем же – от 0 до 9, но их «весовая» характеристика будет качественно другой. Третья позиция определит цифрам порядок «сотен», следующая – «тысяч» и т. д.
Порядковые изменения – это как раз то, что переводит количество в качество и наоборот. Запись цифры в старший разряд – это перевод в новое состояние следующей по иерархии весов ячейки числовой памяти.
По аналогии с записью чисел можно утверждать, что основание системы счисления и диапазон изменения параметров определяют количество стратификационных уровней. Для десятичной системы качественные кванты или «весовые страты» – это единицы, десятки, сотни, тысячи и т. д. Конечно же, модели реальных стратификаций могут быть значительно сложнее, ведь они должны учитывать разнообразные комбинаторные варианты взаимосвязей элементов на различных уровнях.
Расчёт количества информации по методу К. Шеннона при наступлении равновероятных событий (или, что эквивалентно, показатель степени для представления двоичного числа) выражается формулой
(6.1)
где
I – количество информации (или показатель степени числа S);
S – число равновероятных событий (или число S).
При стратификационном описании универсума формула практически не видоизменится
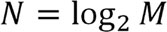
(6.2)
где
N – число универсумных страт.
M – число дискретных состояний универсума;
Проведём стратификационное коэффициентирование универсума. Общее число его дискретных состояний (исключая нулевой уровень)
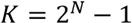
(6.3)
где
K – общее число дискретных состояний;
N – число универсумных страт.
Определим коэффициенты качества (или, что эквивалентно, весовые стратификационные коэффициенты) для U-элементов каждой старты
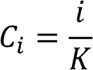
(6.4)
где
i – порядковый номер страты;
Ci – коэффициент качества i-ой страты.
Очевидно, что рис. 195
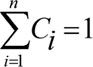
(6.5)
Если для количественного распределения по стратам универсумных элементов TC провести операцию нормировки
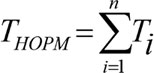
(6.6)
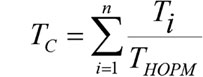
(6.7)
то наличие определённого нормированного количества элементов на стратах позволит получить уникальную качественную характеристику любого варианта распределения элементов по стратам
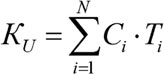
(6.8)
где
N – число универсумных страт;
Ci – коэффициент качества i-ой страты;
Ti – количество элементов (состояний) на i-ой страте.
Это порядок получения числовой «поэлеменно смешанной» информационно-материальной иерархии стратификационных коэффициентов, представляющий следующие ряды:
– для 2U: C1=0,33(3); C2=0,66(6);
– для 3U: C1=0,1429; C2=0,2857; C3=0,5714;
– для 4U: C1=0,06(6); C2=0,13(3); C3=0,26(6); C4=0,53(3) и т. д.
При таком коэффициентировании, например, коэффициент 0,33(3) говорит о том, что данная страта содержит соответствующую коэффициенту долю ИМ-компонентов.
Между тем, если речь ведётся преимущественно об информационном состоянии ОЯП, то алгоритм расчёта весовых характеристик качества объектов должен включать в себя статистику не столько элементного, сколько информационного трафика (величины информационного потока) этих элементов, то есть «долю» структурных связей (связок и/или ссылок) между элементами по каждой универсумной страте.
Реальный алгоритм коэффициентирования, рассматриваемый далее, должен использовать именно «информационную долю», причём долю относительную, характерную именно для своего стратификационного положения. После проведения расчёта получим следующие ряды:
– для 2U: C1=0,25; C2=0,75;
– для 3U: C1=0,1112; C2=0,3333; C3=0,5556;
– для 4U: C1=0,0625; C2=0,1875; C3=0,3125; C4=0,4375 и т. д.
Очевидно, что в этом (пусь и немного усложнённом) варианте расчёта мы получаем более растянутую щкалу качественных характеристик.
Рассмотрим методику расчёта качества универсума более подробно на примере социальных систем.
В социологии предлагалось много критериев прогресса. Среди них – производительность труда, обилие материальных благ, свобода личности, развитие морали и т. д.
При характеристике критериев общественного прогресса нужно учитывать, что общество состоит из ряда сфер и поэтому целесообразно ставить вопрос о критериях прогресса в каждой из этих сфер. А в каждой из этих сфер есть свои подсистемы, имеющие свои критерии прогресса…
Общественный прогресс характеризуется комплексом критериев. Каждый отдельно взятый критерий – необходим, но недостаточен. Лишь весь комплекс этих критериев позволяет адекватно оценить характер эволюции общества [32, 293].
Теоретически некоторый расчёт по «комплексам критериев» вполне возможен, но на практике сбор такой статистики и её обработка, особенно в социальных суперсистемах, пока не представляется реальной. Во-первых, нет единой методологии такого расчёта, во-вторых, элементы социальных структур обладают повышенной динамикой и в любое время легко могут перемещаться по стратам.
Факт отсутствия методологии основывается на отсутствии в различных MEST-системах определения «качества» ОЯП единого критерия стратификации, сравнения и расчёта числовой меры разнокачественностей. Между тем, при различении присущей какой-либо Мере качественной или количественной характеристики ОЯП можно использовать простое, состоящее всего из четырёх пунктов правило Размерности:
1) Односоставная размерность величин (доля, раз, метр, градус) может быть как количественной, так и качественной характеристикой ОЯП единичного универсума (одного элемента супер/системы);
2) Количественная характеристика ОЯП имеет определённую равнокачественную размерность, выраженную определением у всех элементов множества одной разнокачественной размерности (бит/сек., шт./час, м/сек2 и т. п.) и используется минимум для двух элементов;
3) Качественная характеристика ОЯП всегда безразмерна, поскольку выражается соотношением равнокачественных размерностей (доля, раз, процент, балл, коэффициент и т. п.) минимум двух элементов.
4) Как некорректно определять «одним пакетом количества» различные по характеристикам размерности элементы, так и некорректно сравнивать «в одном пакете качества» различные по размерности количественные характеристики.
В соответствии с п.1 правила Размерности, одну и ту же характеристику ОЯП, например, «скорострельность орудия» можно измерить и в абсолютных количественных (выстрелов в минуту) и в относительных качественных (процентное соотношение скорострельности орудия по сравнению с другим образцом) показателях.
Производительность труда (20 [шт./час]) является количественной характеристикой (п.2), а соотношение производительности труда (20 [шт./час]/16 [шт./час]=1,25) различных предприятий – сравнительная качественная характеристика (п.3). Число 1,25 говорит о более высоком качестве работы первого объекта по отношению ко второму.
Нарушение 4-го пункта правила Размерности означает попытку сложения «койко-мест» с «величиной роста телеграфных столбов»[178] и даже позволяет «научно-обоснованно» утверждать, что пять яблок больше трёх килограммов сыра, ведь действительно, пять-то больше трёх!
Что касается динамики межэлементных связей в суперсистемах, к которым относятся и социальные структуры, то, с учётом первого ограничения, более реальным для расчёта статистики является единый для всего универсума, например, пространственно-временной показатель, «суммарное время нахождения элементов на старте» Tc или какой-либо другой. Расчёт по времени Tc учитывает динамику перемещения элементов между стратами, т. е. их функциональную гибкость – способность выполнять разнокачественные (М-И) действия. Для социальной системы характеристикой качества может быть, например, распределение времени нахождения элементов на разлтчных стратах, прекрасно отражающее занятости населения в общественном объединении труда.
Важно определить, что при расчёте числовых характеристик качества первостепенную роль имеет не столько количество элементов, сколько интегральная «весовая» характеристика их связей, то есть степень влияния на результирующее SR-поведение универсума. Именно поэтому для расчёта суммарной качественной характеристики объекта используется ранжированный в соответствии с универсумной логикой вектор стратификационных коэффициентов, присваивающих каждой страте определённый «качественный вес» Cк. Стратификационные коэффициенты Cк отражают МЕРУ – достигнутые уровни обобщения информации о внешней среде, суммарную «мощность информационного трафика» элементов страт U (рис. 6.21б).
Заметим, что другие варианты расчёта весовых коэффициентов возможны, но не должны менять принципиального соотношения расчётных величин. Они могут быть более удобны в каких-то частных, профессиональных, определённых отношениях[179]. При этом, должно соблюдаться основное правило в проведении числового коэффициентирования качественных характеристик: суммарное числовое значение показателя качества всех предыдущих уровней страт должно быть меньше значения показателя качества расчётной страты. Это правило отражает тот самый «скачок» качества, отличающий разнокачественные ОЯП друг от друга. Ведь очевидно, что ОЯП более высокого качества должен обладать свойством или комплексом дополнительных свойств, дающим ему этот «скачок» в виде более высокой оценки качества.
При линейном коэффициентировании интегральный показатель качества KU отражает степень организационной связности элементов U, его способность эффективно отрабатывать воздействия внешней среды. Нормированная сумма произведения времени нахождения элементов на соответствующий стратификационный коэффициент (рис. 6.21в) даёт искомое числовое значение качества объекта КU.
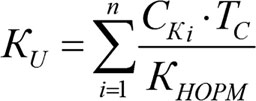
(6.9)
где
n – Количество универсумных страт;
СК – Стратификационные коэффициенты;
TC – Суммарное время нахождения элементов в страте;
КНОРМ – коэффициент нормировки к диапазону числовых значений от 0 до 100 % или от 0 до 1
Число страт дискретизации определяет точность оценок качества – чем их больше, и чем точнее подсчитано суммарное время работы элементов на стратификационных уровнях, тем точнее будет и качественная оценка исследуемого объекта.
Общая алгоритмика получения значений линейных стратификационных коэффициентов (рис. 6.22) для универсума класса N включает:
1) определение весовой разницы между элементами R
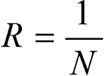
(6.10)
2) Определение стратификационного коэффициента первой страты
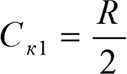
(6.11)
3) Определение числовых значений всех остальных коэффициентов, с учётом весовой разницы между ними:
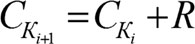
(6.12)
4) Определение коэффициента нормировки КНОРМ полученных значений СКi
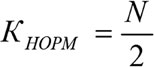
(6.13)
Нормированные коэффициенты качества являются просто переводом аналоговой линейной универсумной диагонали Меры в дискретное представление размерностью N. Рис. 204
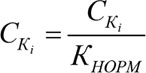
(6.14)
Сумма коэффициентов качества СК должна удовлетворять условию:
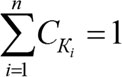
(6.15)
После проведения нормировки формула (6.9) может быть представлена в сокращенном, более оптимальном виде:
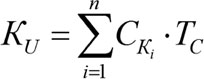
(6.16)
Предельную математическую погрешность показателя качества для любого универсума можно рассчитать по формуле
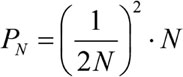
(6.17)
Она составит 6,25 % для универсума класса 4U; 3,125 % для 8U; 1,5625 % для 16U и т. д.
На основании приведённого алгоритма коэффициентирования для любого универсума могут быть получены стандартные значения стратификационных коэффициентов соответствующей степени точности.
В принципе, следует говорить о двух взаимосвязанных характеристиках – абсолютном качестве универсума как такового, и об относительном показателе качества. Абсолютное качество должно учитывать распределение расчётных элементов универсума по стратам (именно о нём здесь и далее и идёт речь), а относительное качество – это степень соответствия универсума конкретным условиям внешней среды. Чем более точно в требованиях к качеству учтены условия эксплуатации во внешнем мире, тем более высоким будет относительное качество системы[180].
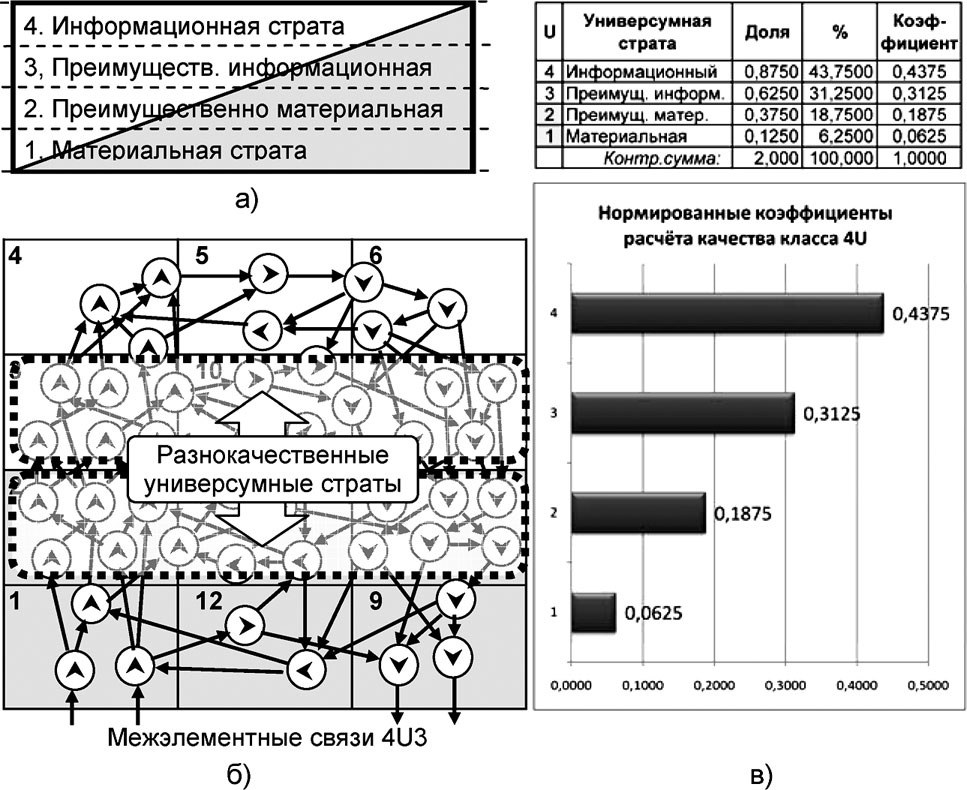
Рис. 6.22. Коэффициентирование качества универсума класса 4U
а) качественное распределение страт универсума;
б) универсумные фреймы и межэлементные связи;
в) весовые значения коэффициентов качества
Разберём алгоритмику и порядок полного цикла расчёта качественных характеристик различных объектов из областей прикладного характера: технической, армейской и фирменно-корпоративной сфер жизнедеятельности социальных систем.
Данный текст является ознакомительным фрагментом.